Självstudiekurs i Mandelbrot- och Julia-fraktaler för vetgiriga elever
av
Ingvar Kullberg
(OBS! Denna sida är fortfarande att betrakta som under uppbyggnad.)
Inledning:
Denna självstudiekurs är ämnad dels för elever på grund- och gymnasieskolan, men även för alla andra i detta avlånga land som är nyfikna och vill lära sig grunden om mandelbrot- och julia fraktaler (i omvänd ordning). Kursen består av två delar:
I) Lek med den fria programvaran Xaos. Xaos är ett program med s k öppen källkod och finns för plattformarna macOS, LINUX och Windows. Att programmet är gratis samt att det finns för alla plattformar är orsaken till att jag byggt upp kursen kring detta program.
II) Allvarlig teori och matte. Detta bygger på att ärade elev läser mitt "stora" kompendium som jag skrev 1993 och som jag nu gjort om till en pdf-fil och lagt ut på nätet:
Vägen till mandelbrotmängden (pdf)
Introduktion till matematiken bakom mandelbrot & julia-fraktalerna för folk med grundskolekompetens i matematik. Ett måste för alla som är nyfikna på fraktaler men saknar förkunskaper. Avsett för dubbelsidig utskrift, drygt 40 sidor innehållande ett 30-tal illustrationer.
Jag har lagt upp den teoretiska delen av kursen som en två veckors icke betungande studieplan. En halvtimmes plugg per dag bör räcka. Men när ni kommer till denna del gäller det att ni har Vägen till mandelbrotmämgden öppen i en flik, eller ännu bättre, dubbelsidigt utskriven i handen. Sitter ni vid datorn, bör ni ha Xaos igång. För er som eventuellt köpt kompendiet (med det giftgula omslaget) innan jag lade ut den som en pdf-fil på nätet, gäller att sidhänvisningarna inte stämmer. Det beror på att i er version är sidan "1" första sidan av första kapitlet, medan här sidnumreringen börjar på omslagssidan.
I) Lek med Xaos:
Installation (Windows): Klicka på installfilen. Programmet går snabbt och lätt att installera.
Att zooma: När du startat programmet och maximerat dess fönster, har du en oförstorad version av mandelbrotmängden. Förstora, gör du det genom att peka med musen på ett intressant område i gränsen till mandelbrotfiguren och hålla vänster musknapp nertryckt. Du kan zooma ut igen genom att trycka ner höger musknapp. Vill du återställa fönstret (till när du startade programmet), välj Reset to defaults under Fractal menu.
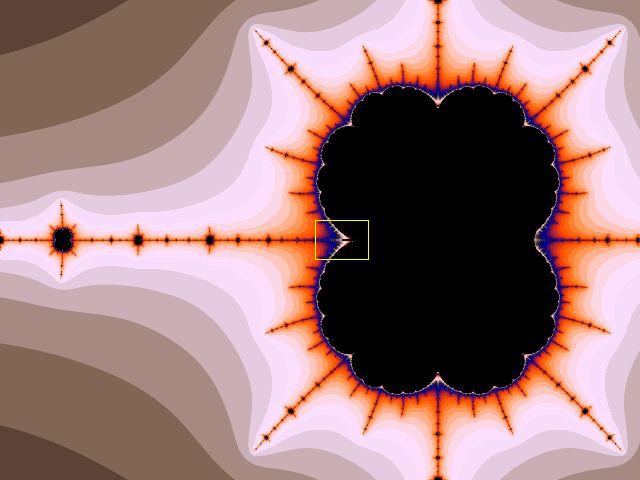
Iterations tal: När du zoomat ner en bit kan det se ut som bilden nedan till vänster, där programmet utför maximalt 170 s k iterationer. Går du till Iterations under Calculation menu och ökar du detta tal till 1000 dyker fler mönster fram ur det svarta som framgår av bilden till höger.
I själva verket kan iterationstalet med fördel ökats ytterligare. Gör du det försvinner de svarta ögonen i stjärnorna till höger om ravinen. Mer om hur och varför, kan du läsa i detta 3-sidiga pdf-dokument (1 sida text och 2 sidor illustrativa bilder).
Lek med juliamängder: Juliamängder kan man skapa genom att under Fractal menu välja bort Mandelbrot mode. Då får man upp en dialogruta där du kan skriva in två tal. Från början står det noll i båda. Klickar du OK får du upp en svart cirkel med färgade band runt om kring. M a o väldigt ointressant. Skriver du in -2 i det vänstra fältet får du en rak linje med en massa lopar runt omkring, bara lite mer intressant än cirkeln och fortfarande ingen fraktal. För alla andra värden du skriver in i rutorna (den ena eller båda) får du dock en fraktal. Men det är väldigt svårt att på detta vis hitta en vacker sådan. Dessutom uppfylls fördomarna om att dom som gör fraktaler sitter och skriver in en massa siffror. Därför lämnar vi nu detta sätt att göra juliafraktaler för ett mycket mycket smartare och helt underbart sätt, så fortsätt nu och häng med på resan. Alltså,
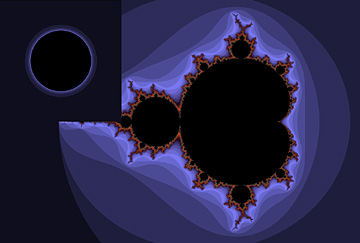
1) Gå till Calculation menu och välj Fast julia mode så får du en svart diskus uppe i vänstra hörnet (bilden nedan till vänster).
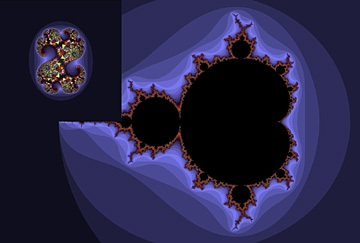
2) Tryck ner vänster musknapp och dra runt i bilden utanför och inanför mandelbrotfiguren och se vad som hände med bilden i övre vänstra hörnet. I högra bilden nedan ser du vad som händer när man klickat någonstans i bakregionen vid gränsen till mandelbrotmängden.
3) När du är nöjd, släpp musknappen och gå till Fractal menu och välj bort Mandelbrot mode och klicka OK i dialogrutan. Dom båda talen som är inskrivna i dialogrutan är koordinaten i bilden av mandelbrotmängden du släppte musknappen (eller klickade sist) under Fast julia mode. Bilden du hade uppe i övre vänstra delen kommer nu upp som huvudbild.
4) Bilden är dock ocentrerad. Det kan du råda bot på genom att gå till View under Fractal menu. Där det (troligen) står -0758 (första rutan efter Center), skriver du in "0" och klickar OK..
5) Om du plockar din julia från en inzoomad bild av mandelbrotmängden, är juliamängden inzoomad i motsvarande grad. Det är en av de lite knäppa sakerna med Xaos. Det kan du emellertid råda bot på genom att under förgående punkt nämnda Fractal menu - View skriva in ”2.5” i Radius. Detta samtidigt som du skriver in ”0” i dom båda rutorna efter Center för att centrera figuren. Ett alternativ sätt är att zooma ut genom att peka i bilden och hålla höger musknapp nere. Överhud taget kan du zooma ut och in i din julia-fraktal av hjärtans lust.
Bailout: I mina fyra första exempelbilder ovan, kanske du noterat att gränserna mellan färgnyanserna kommer lite mer jämt och harmoniskt än vad dom gör i programmets grundinställning. Vad jag gjort är att ändra bailouten från 4 (minimum) till 100. Det kan du göra under Calculation - Bailout. Mer om Bailout senare.
Spara dina alster: Du kan spara dina alster på två sätt:
1) Som en parameter-fil vilken kan laddas tillbaka till Xaos. En parameter fil är i själva verket en textfil som innehåller instruktioner till Xaos hur den skall återskapa ditt mästerverk. Alternativt, om det inte är ett mästerverk, kan du fortsätt jobba med bilden. File - Save för att spara och File - Load för att ladda tillbaka den. Observera att du tyvärr måste lägga till filändelsen ”.xpf” själv. Gäller Windows versionen.
2) Som en png-fil som du kan läsa in i något grafiskt program som t ex Photoshop, eller Gimp, där du sen kan manipulera vidare med den, ändra filformat etc. File - Save image för att spara som en png-fil. Observera att du även här tyvärr måste lägga till filändelsen, i detta fall ”.png”, själv. Gäller Windows versionen.
Anti-aliasing: Om du drar upp en bild för publisering, skall du ha Antialiasing under Filter menu invald. Anti-aliasing är inget filter men ett sätt eliminera blurrighet. Mer om anti-aliasing kan du läsa här. Titta i alla fall på bilderna.
Buggar: Jag har hittat två buggar i Xaos
1) Xaos har vänt på imaginäraxeln så att när du knappar i ett värde i Julia seed där imaginär-värdet inte är noll, t ex -0.75 + 0.1i, tar Xaos det som -0.75 - 0.1i. Figuren blir densamma, fast roterad runt den reella axeln (horisontalaxeln). När du däremot använder dig av Fast julia mood blir slutresultatet helt rätt, förutsatt att du inte ”rättar till" i dialogrutan innan du klickar OK.
2) Fractal - Formula: Mandelbrot^6 visar i själva verket Mandelbrot^9.
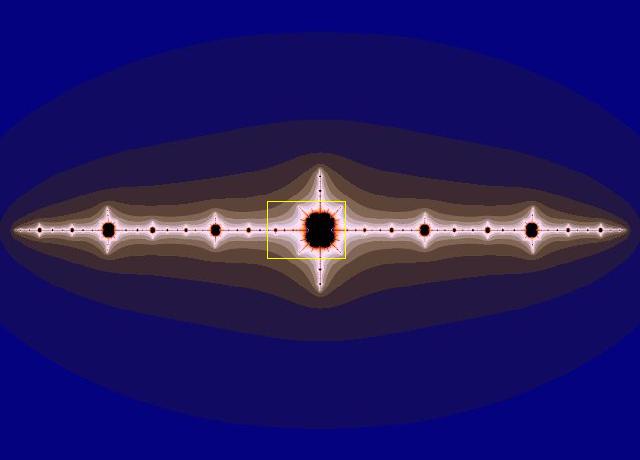
Inspirerande zoom-sekvenser: För en demonstratiom av den i oändlighet ökande komplexiteten i gränsen till mandelbrotmängden, klicka respektive bild nedan och gå till sidan 4 i respektive pdf-dokument (jo du får givetvis läsa texten också),
Zoom-sekvensen till den vänstra bilden går att djupt så Xaos, och dom flesta program inte hänger med, beroende på att dom inte kan hantera tillräckligt långa decimaltal. Jag har använt fractal eXtreme, världens bästa program för extrema djupzoomer i (gränsen till) mandelbrotmängden. för det motivet. Men du kan hänga med en bra bit i sekvensen med Xaos. Den högra bilden är inte så djupt zoomad. För den bilden har jag använt Ultra Fractal, min mest använda programvara.
Det finns mycket mer i Xaos. Bara prova och experimentera och klicka på Hjälp vid behov. Jag är ingen expert på detta program därför att jag allra mest använder ovan nämnda program (fx och UF). Det förstnämnda (fractal eXtreme) är världens bästa program för extrema djupzoomer i (gränsen till) mandelbrotmängden. Det är också ett väldigt enkelt program med en mycket pedagogisk hjälpfil. Tyvärr så är emellertid inte dessa program gratis.
II) Nu börjar allvaret:
(alla kapitelhänvisningar här avser Vägen till mandelbrotmängden om inget annat anges). Punkterna nedan är avsedda att stödja (coacha), d v s motivera ärade fraktal-student att läsa kapitel för kapitel. Lite komplementerande saker finns här också.
1) Första kapitlet förklar vad en fraktal är i största allmänhet. Detta med hjälp av Helge von Koch snöflinga. Ta gärna en titt på Wikipedia, särkilt dess illustrationer. Ännu bättre tycker jag att engelska Wikipedia är. Förutom Helge von Kock snöflinga finns det en ännu äldre monsterfigur, Sierpinskitriangeln. ta gärna en titt på den.
2) Om du vet vad tallinjen är för något, kan du hoppa över kapitel 2. Annnars läs detta mitt kortaste kapitel och/eller fråga din mattelärare.
3) Nu kommer kapitel 3 om iteration och 4 om komplexa tal, Dessa är nyckelkapitlen för den matematiska förståelsen av "mandel och julia". Läs kapitel 3 på måndag, 4 på tisdag, 3 igen på onsdag, och 4 igen på torsdag.
4) På fredag kan du så läsa syntesen av kapitel 3 och 4, kapitel 5 Iteration i det komplexa talplanet.
5) Efter lek med Xaos under helgen, och förhoppningsvis också vistelse i naturen (naturen vimlar av fraktala mönster) tar vi på måndag itu med det korta torra kapitel 6, Det kaotiska intervallet.
6) Nu är det tisdag och det börjar brännas. Kapitel 7 Färgerna då? beskriver hur ett mandelbrot och julia-program förbinder olika pixlar med med olika komplexa tal på det komplexa talplanet (pixlarna är bildpunkterna som bygger upp skärmen). Sedan beskrivs principen hur pixlarna färgsätts.
Uppgift: Ärade läsare uppmanas att med användande av Xaos, köra upp dom tre juliamängder som exemplifieras i kapitlet. Du knappar in värdena på real- och imaginär- delen i dialogrutan du får upp när du under Fractal menu väljer bort Mandelbrot mode. Observera dock vad jag skrev under "Buggar" (gäller tredje juliamängden). Sedan kan du centrera under Fractal menu - View. Du kommer givetvis att få andra färger än dom i kompendiet eftersom bilderna där är i svart och vitt. Den andra juliamängden, den för c = -2 har du tidigare kört upp i Xaos om du under ”Lek med juliamängder” aktivt följt med i ”Xaos-kursen” under del I ovan. Där såg du också att färgerna bildade en ”massa lopar runt omkring” till skillnad hur dom kommer i figur 9 i kompendiet. Det beror på att den s k escape-radien i Xaos (och i dom flesta fraktalprogram) är satt på lägsta värde man kan ha utan att riskera att få sina mängder avklippta, vilket är 2. Jag har i figur 9 och i alla andra illustrationer i kompendiet ökat denna radie till 10. Det är här vår Bailout kommer in. Denna är detsamma som escape-radien i kvadrat. Så Bailout = 4 motsvarar en escape-radie på 2 och en Bailout på 100 är det samma som escape-radien 10. Vad det hela handlar om är att när man man använder Pythagoras sats för att räkna ut absolutbeloppet på variabeln ”z”, ger man tusan i att dra roten ur kvadraten på hypotenusan. Detta snabbar avsevärt upp uträkningen av en bild.
7) Onsdagens lektion: När du läser eller läst om dom olika juliamängderna som exemplifieras i kapitel 8 Några juliamängder kan du köra upp dessa i Xaos genom att knappa in dom värden på konstanten ”c” som anges i beskrivningen. När du kommer till sidan 30 och fått fram juliamängden i figur 18, kan du själv zooma in mot centrum för att se ”blomkålet” i mitten. Än en gång, observera dock vad jag skrev under "Buggar" (gäller gäller figurer 17 - 20).
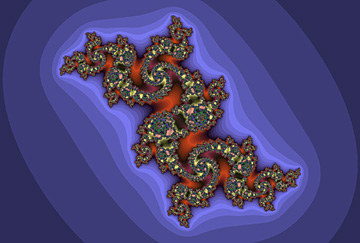
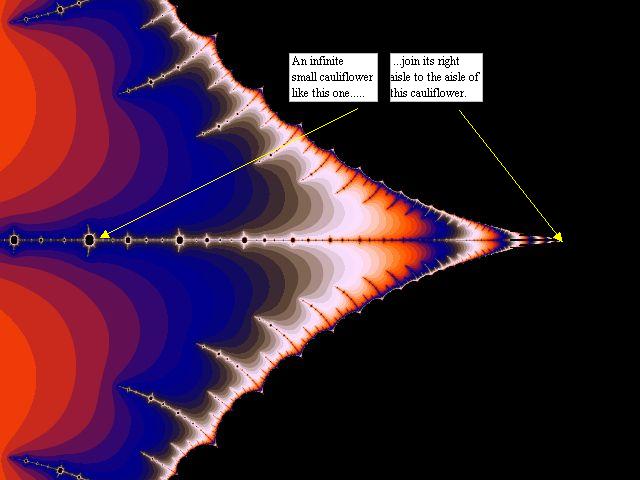
Beträffande denna sista komplexa juliamängd. Om du inte förstår varför jag kallar den det Lesbiska mysteriet, kolla nedanstående tre illustrationer, 2:a och 3:e bilden är in-zoomningar i den första.
Dessa tre bilder är körda i Ultra Fractal och illustrationerna ingår i article 4 i en serie artiklar jag skrev på engelska för några år sedan. Mer om dom senare. Ni kan lätt köra upp denna juliamängd med Xaos om ni väljer bort Mandelbrot mode under Fractal menu och knappar in -1.75 i första rutan efter Julia seed.
8) Äntligen är vi framme vid kapitel 9 Mandelbrotmängden. Läs definitionen på sidan 33 noggrant. När ni läst kapitlet, meditera över figur 22.
Uppgift: När ni har figur 22 i er inre syn, starta Xaos, gå till Calculation menu och välj Fast julia mode. Tryck ner vänster musknapp och rör muspekaren till dom ställen pilarna i figur 22 pekar på och kontrollera att ni får upp ungefär samma juliamängder. Försök observera att centrum av den juliamängd som visas i övre vänstra halvan har samma färg som den färg du håller muspekaren över i bilden av mandelbrotmängden. Beträffande färgerna, läs nu gärna det lilla pdf-dokumentet om färgerna runt mandelbrotmängden, som du kanske redan kikat på, en gång till. Titta särskilt på bilderna.
9) Nu är vi framme vid kapitel 10, det sista riktiga kapitlet i kompendiet, Det Lesbiska mysteriet. Kapitlet är egentligen en fortsättning på föregående kapitel om mandelbrotmängden. Här förklaras tillkomsthistorien bakom den sofistikerade juliamängden sist i kapitel 8 med det "lesbiska mysteriet".
Uppgift: Starta Xaos och gör själv inzoomningen som visas i figurer 23 - 29. Gör gärna en mer närgången zoom till minimandelbroten i figur 29. OBS, ni måste höja det maximala iterationsantalet (under Calculation) till åtminstone 1000 för att dom djupa nivåerna skall bli ”renkörda" (utan svarta artifakter). Därefter välj Fast Julia mood och gör en juliamängd genom att klicka baken på minibroten. Gör även andra juliamängder genom att klicka på andra ställlen innaför och utanför den lilla svarta babyn ;)
Appendix) Några handgripliga matteexempel:
Mandelbrotmängden definieras som dom parametrar ”c” för vilken variabeln ”z” för evigt rör sig inom en radie av 2 under den dynamiska processen
z -> z^2 + c
när z = 0 är startvärde. Detta kan skrivas som,
0 -> 0^2 + c = c -> c^2 + c -> (c^2 + c)^2 + c, etc.
Att bestämma om en punkt på c-planet tillhör mandelbrotmängden eller inte kräver i dom flesta fall beräkningar med långa decimaltal. Dessa blir längre och längre ju djupare vi zoomat in. Det finns dock vissa punkter som är heltal, och där man kan använda "papper och penna". Tar vi dom från mittlinjen, behöver vi inte ens bry oss om komplexa tal (imaginärdelen är noll). Nedan ska vi titta på några sådana "hardcore" exempel, så häng med nu:
1) Tillhör c = 1 mandelbrotmängden?
Låt oss testa:
0 -> 0^2 + 1 = 1 -> 1^2 + 1 = 2 -> 2^2 +1 = 5 -> 5^2 +1 = 26, etc.
Tydligen tillhör INTE c = 1 mandelbrotmängden eftersom variabeln ”z” mycket snabbt rusar iväg mot oändligheten. Detta betyder att Juliamängden för c = 1 är totalt osammanhängande (en s k cantormängd). I själva verket är det så att så fort variabeln ”z” passerat radien 2, det må vara efter t ex 3, 33 eller 3 miljoner iterationer, rusar variabeln med en ökande acceleration mot oändligheten. I bilden nedan ser vi resulterande juliamängd (dom följande illustrationerna är körda med Ultra Fractal),
2) Tillhör c = 0 mandelbrotmängden?
Låt oss testa:
0 -> 0^2 + 0 = 0 -> 0^2 + 0 = 0 etc.
Japp! Och tillhörande juliamängd är enhetcirkeln, se kapitel 5 Iteration i det komplexa talplanet. Parameter c = 0 är belägen i ”centrum” av den hjärtformade kroppen (se figur 22 sidan 35). Alla juliamängder genererade av av en parameter belägen inuti den hjärtformade kroppen ger upphov till juliamängder där en av de två fixpunkterna är attraktiv (attraherar orbits från insidan av sin slutna domän).
3) Tillhör c = -1 mandelbrotmängden?
Låt oss testa igen:
0 -> 0^2 + (-1) = -1 -> (-1)^2 + (-1) = 1 - 1 = 0 -> 0^2 + (-1) = -1, etc.
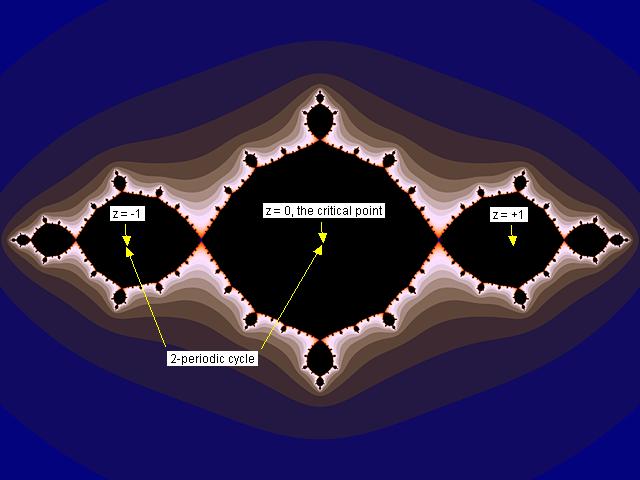
Här är orbiten av z = 0 omedelbart fångad i den 2-periodiska cykeln 0 -> -1 -> 0 -> -1, etc. I själva verket är c = -1 centrum av huvudet till mandelbrotmängden. Alla c-värden från huvudet till mandelbrotmängden ger upphov till ifyllda juliamängder till vilken hör en 2-periodisk attraktiv cykel. Se sidan 25, figur 12 sidan 26, samt bilden nedan,
4) Tillhör c = -2 mandelbrotmängden?
Låt oss testa igen:
0 -> 0^2 + (-2) = -2 -> (-2)^2 + (-2) = 4-2 = 2 -> 2^2 + (-2) = 4 - 2 = 2, etc.
Vi har alltså orbiten: 0 -> -2 -> 2 -> 2, etc. Parameter c = -2 är den allra yttersta spetsen på spiken på mandelbrotmängden.. Juliamängden för denna c-parameter är en rak linje frän z = - 2 till z = +2. Men det har du redan läst om i kapitel 6 Det kaotiska intervallet.
5) Tillhör c = i mandelbrotmängden?
0 -> 0^2 + i -> i -> i^2 + i = -1 + i -> (-1 + i)^2 + i = (1 – i – i + i^2) + i = (1 – 2i –1) + i = -i -> (-i)^2 + i = -1 + i, etc.
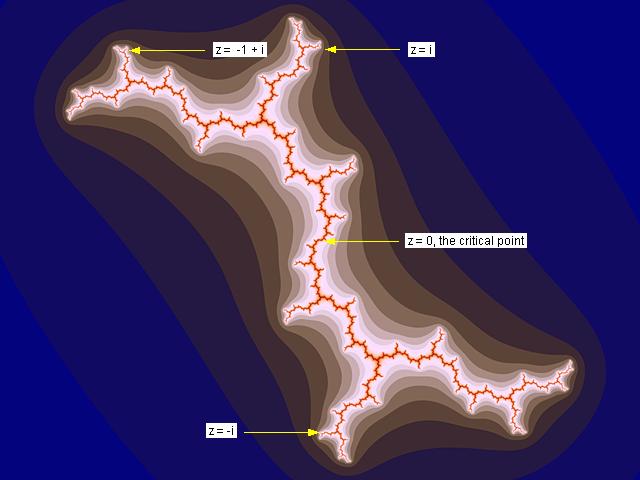
Vi har alltså orbiten: 0 -> i -> -1 + i -> -i -> -1 + i -> -i, etc. Efter 2 iterationer är vi fångade i en (repellerande) 2-periodisk cykel: -1 + i -> -i, etc. M ao c = i tillhör helt klart mandelbrotmängden eftersom orbiten av z = 0 inte rusar mot oändligheten. Precis som c = -2 är c = i den allra yttersta spetsen på en gren. I detta fallet är spetsen den yttersta spetsen på den högra grenen av ”Y-et” längst upp. I själva verket är spetsen den yttersta spetsen av en mycket långsam högervridande spiral och nås efter att ha zoomat ner i spiralen oändligt många varv!!! Juliamängden för denna c-parameter visas i bilden nedan.,
6) Tillhör c = -i mandelbrotmängden?
Vi gissar ”ja” eftersom denna punkt är c = i speglad runt den reella axeln. Så låt oss kolla orbiten av den kritiska punkten z = 0 för denna c-parameter:
0 -> 0^2 + (-i) = -i -> (-i^2) + (-i) = -1 – i -> (-1 – i)^2 + (-i) = (1 + i + i + (-i)^2) + (-i) = 1 + 2i –1) + (-i) = i -> i^2 + (-i) = -1 – i, etc.
Orbiten är alltså: 0 -> -i -> -1 - i -> i -> -1 - i -> i, etc. Lite andra tecken m a o. Resulterande juliamängd är, som vi kunde väntat oss, spegelvänd jämfört med den i föregående bild.
Sammanfattningsvis:
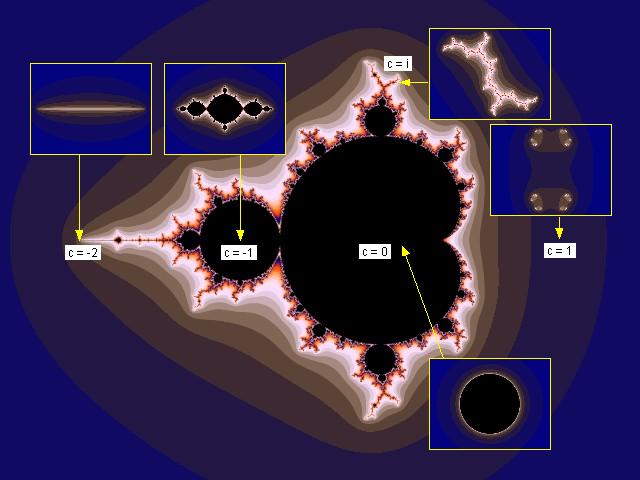
I bilden nedan, visas alla juliamängder som är resultatet av ovanstående exempel. Pilarna är dragna till de ställen i parameterplanet, d v s c-planet, som våra exempelparametrar är hämtade från. Ta gärna en titt på figur 22 sidan 35 i Vägen till mandelbrotmängden samtidigt som du betraktar nedanstående bild,
Vidare förkovran
Har du hängt med så långt och känner dig inspirerad, rekommenderar jag varmt en artikelserie jag skrev för några år sedan,
The chaotic series of fractal articles
Serien består av fler än trettio illustrerade artiklar. Dom tre ”Intro-artiklarna” är en direkt översättning av kapitel 3 - 5 i Vägen till mandelbrotmängden, så du kan börja direkt med article 1 Level sets. Observera att alla artiklarna INTE är matematiska. Artiklar 10 - 14 behandlar dom kombinatoriska lagarna för grenverket i mandelbrotmängden. Har du läst dom, kan du med stor säkerhet se var någonstans i mandelbrotmängden en bild från denna är inzoomad.
Mot högre parameterrymder: I Xaos, liksom i dom flesta andra program för mandelbrot- och julia-fraktaler, finns motsvarigheter för mandelbrot- och julia-mängder för högre gradtal, dvs z -> z^3 + c, z -> z^4 + c, z -> z^5 + c, etc. Men medan z -> z^2 + c representerar ALLA s k polynom av andra graden, representerar z^3 + c endast en del av alla kubiska polynom och z^4 + c en ännu mindre del av alla polynom av 4:e graden. Den fulla motsvarigheten till iterationformeln för kvadratiska polynom (z -> z^2 + c) för kubiska polynom är z -> z^3 - 3a^2 z + b, med dom kritiska punkterna z = +a och z = -a. Eftersom vi har två komplexa parametrar, ”a” och ”b”, d v s vi har fyra axlar a_reell, a_imag, b-reell, och b_imag får vi en fyrdimensionell parameterrymd. Alltså en dimension mer än rummet. Men mer om detta kan ni läsa på min sida,
Från artikel 16 och framåt i min artikelserie är ämnet dessa parametrrymder för ”cubics” och ännu högre parameterrymder.
Ännu högre parameterrymder har du exempel på nedan där två 3D-snitt av den sex-dimensionella parameterrymden för fjärdegrads polynom (quartics) visas,
Iterations formeln för quartics är z -> z^4 + 2[ab - (a + b)^2]z^2 + 4ab(a + b)z + c, kritiska punkter, z = a, z = b, och z = -(a + b) som ger upphov till mängderna M1, M2, och M3 då dom har begränsade orbits. Det är dessa mängder som representeras av dom tre färgerna i bilderna ovan. Men detta är överkurs. Vill ni veta mer om quartics, läs dom tre sista artiklarna i min artikelserie! Bilderna är körda med en formel för Ultra Fractal. programmerad av en god vän till mig.
Om mig själv
Jag som gjort denna sida är ingen matematiker. Jag bara låtsas. Hur jag kom att syssla med fraktaler på min fritid kan ni läsa i inledningen till en populärvetenskaplig artkel jag blev ombedd att skriva för några år sedan. Den finns länkad till i min ocoola svenska ingångsportal, där, förutom länkar till mina fraktalsidor, även finns länkar till mina andra intressen, Paninis sanskritgrammatik, Ales stenar, fiktion och verklighet, etc.
Synpunkter på denna lilla kurs mottages tacksamt av,
Unika besökare sedan 2010.01.01